Research

Mathematical theory of the attention mechanism and its applications in operator learning

Blog posts

• Provable approximation capacity of the Galerkin-type attention (a linear complexity attention without softmax)

References

1. Guo, R., Cao, S. and Chen, L. (2023) “Transformer Meets Boundary Value Inverse Problems,” in Eleventh International Conference on Learning Representations (ICLR 2023). Available at: https://openreview.net/forum?id=HnlCZATopvr.

   @inproceedings{GuoCaoChen2022inverse,
     author = {Guo, Ruchi and Cao, Shuhao and Chen, Long},
     booktitle = {Eleventh International Conference on Learning Representations (ICLR 2023)},
     year = {2023},
     keywords = {Machine Learning (cs.LG), Numerical Analysis (math.NA), FOS: Computer and information sciences, FOS: Computer and information sciences, FOS: Mathematics, FOS: Mathematics, 35R30, 65N21, 65R10, 68T07},
     title = {Transformer Meets Boundary Value Inverse Problems},
     primaryclass = {cs.LG},
     eprint = {2209.14977},
     archiveprefix = {arXiv},
     arxiv = {https://arxiv.org/abs/2209.14977},
     url = {https://openreview.net/forum?id=HnlCZATopvr},
     code = {https://github.com/scaomath/eit-transformer},
     copyright = {arXiv.org perpetual, non-exclusive license}
   }

2. Cao, S. (2021) “Choose a Transformer: Fourier or Galerkin,” in 35th Conference on Neural Information Processing Systems (NeurIPS 2021). Available at: https://openreview.net/forum?id=ssohLcmn4-r.

   @inproceedings{Cao2021transformer,
     title = {Choose a Transformer: Fourier or Galerkin},
     author = {Cao, Shuhao},
     booktitle = {{35th Conference on Neural Information Processing Systems (NeurIPS 2021)}},
     year = {2021},
     primaryclass = {cs.LG},
     arxiv = {https://arxiv.org/abs/2105.14995},
     code = {https://github.com/scaomath/galerkin-transformer},
     url = {https://openreview.net/forum?id=ssohLcmn4-r},
     note = {http://scaomath.github.io/assets/pdfs/gt_poster_neurips2021.pdf}
   }

   In this paper, we apply the self-attention from the state-of-the-art Transformer in Attention Is All You Need for the first time to a data-driven operator learning problem related to partial differential equations. An effort is put together to explain the heuristics of, and to improve the efficacy of the attention mechanism. By employing the operator approximation theory in Hilbert spaces, it is demonstrated for the first time that the softmax normalization in the scaled dot-product attention is sufficient but not necessary. Without softmax, the approximation capacity of a linearized Transformer variant can be proved to be comparable to a Petrov-Galerkin projection layer-wise, and the estimate is independent with respect to the sequence length. A new layer normalization scheme mimicking the Petrov-Galerkin projection is proposed to allow a scaling to propagate through attention layers, which helps the model achieve remarkable accuracy in operator learning tasks with unnormalized data. Finally, we present three operator learning experiments, including the viscid Burgers’ equation, an interface Darcy flow, and an inverse interface coefficient identification problem. The newly proposed simple attention-based operator learner, Galerkin Transformer, shows significant improvements in both training cost and evaluation accuracy over its softmax-normalized counterparts.
   
   

   

Theory and applications of virtual element method for interface problems

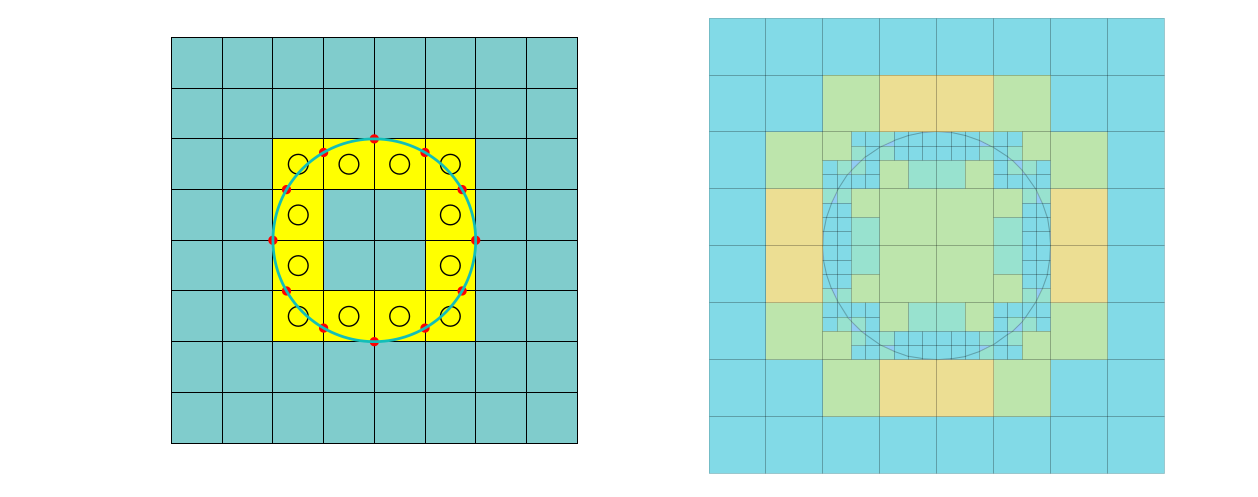
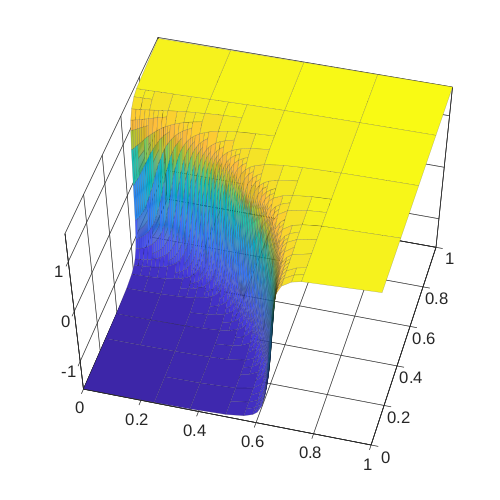
Blog posts

• Implementing data structures for polygonal finite elements
• Remarks and notes on the trace theorems on Lipschitz domains

References

1. Cao, S., Chen, L., Guo, R. and Lin, F. (2022) “Immersed Virtual Element Methods for Elliptic Interface Problems in Two Dimensions,” Journal of Scientific Computing, 93(1), pp. 1–41. doi: 10.1007/s10915-022-01949-x.

   @article{CaoChenGuoLin2022immersed,
     title = {Immersed Virtual Element Methods for Elliptic Interface Problems in Two Dimensions},
     author = {Cao, Shuhao and Chen, Long and Guo, Ruchi and Lin, Frank},
     year = {2022},
     month = aug,
     journal = {Journal of Scientific Computing},
     volume = {93},
     number = {1},
     pages = {1-41},
     eprint = {2108.00619},
     archiveprefix = {arXiv},
     primaryclass = {math.NA},
     doi = {10.1007/s10915-022-01949-x},
     arxiv = {https://arxiv.org/abs/2108.00619}
   }

2. Cao, S., Chen, L. and Guo, R. (2021) “A Virtual Finite Element Method for Two-Dimensional Maxwell Interface Problems with a Background Unfitted Mesh,” Mathematical Models and Methods in Applied Sciences (M3AS), 31(14), pp. 2907–2936. doi: 10.1142/S0218202521500652.

   @article{CaoChenGuo2021Maxwell,
     title = {A Virtual Finite Element Method for Two-Dimensional Maxwell Interface Problems with a Background Unfitted Mesh},
     author = {Cao, Shuhao and Chen, Long and Guo, Ruchi},
     journal = {Mathematical Models and Methods in Applied Sciences (M3AS)},
     volume = {31},
     number = {14},
     pages = {2907-2936},
     year = {2021},
     doi = {10.1142/S0218202521500652},
     arxiv = {https://arxiv.org/abs/2103.04582}
   }

3. Cao, S. (2021) “A simple virtual element-based flux recovery on quadtree,” Electronic Research Archive, 29(6), pp. 3629–3647.

   @article{Cao2020quadtree,
     title = {A simple virtual element-based flux recovery on quadtree},
     author = {Cao, Shuhao},
     journal = {Electronic Research Archive},
     volume = {29},
     number = {6},
     pages = {3629-3647},
     year = {2021},
     primaryclass = {math.NA},
     arxiv = {https://arxiv.org/abs/2006.05585},
     code = {https://github.com/lyc102/ifem/tree/master/research/polyFEM}
   }

4. Cao, S. and Chen, L. (2019) “Anisotropic error estimates of the linear nonconforming virtual element methods,” SIAM Journal on Numerical Analysis. SIAM, 57(3), pp. 1058–1081.

   @article{CaoChen2019nonconforming,
     title = {Anisotropic error estimates of the linear nonconforming virtual element methods},
     author = {Cao, Shuhao and Chen, Long},
     journal = {SIAM Journal on Numerical Analysis},
     volume = {57},
     number = {3},
     pages = {1058--1081},
     year = {2019},
     publisher = {SIAM},
     arxiv = {https://arxiv.org/abs/1806.09054}
   }

   A refined a priori error analysis of the lowest order (linear) nonconforming Virtual Element Method (VEM) for approximating a model Poisson problem is developed in both 2D and 3D. A set of new geometric assumptions is proposed on shape regularity of polytopal meshes. A new error equation for the lowest order (linear) nonconforming VEM is derived for any choice of stabilization, and a new stabilization using a projection on an extended element patch is introduced for the error analysis on anisotropic elements.
   
   
5. Cao, S. and Chen, L. (2018) “Anisotropic error estimates of the linear virtual element method on polygonal meshes,” SIAM Journal on Numerical Analysis. SIAM, 56(5), pp. 2913–2939.

   @article{CaoChen2018anisotropic,
     title = {Anisotropic error estimates of the linear virtual element method on polygonal meshes},
     author = {Cao, Shuhao and Chen, Long},
     journal = {SIAM Journal on Numerical Analysis},
     volume = {56},
     number = {5},
     pages = {2913--2939},
     year = {2018},
     publisher = {SIAM},
     arxiv = {https://arxiv.org/abs/1806.09069}
   }

Acknowledgement

• This research was supported in part by the National Science Foundation under grants DMS-1913080 and DMS-2136075.

   

Finite element methods for problems related to Maxwell’s equations

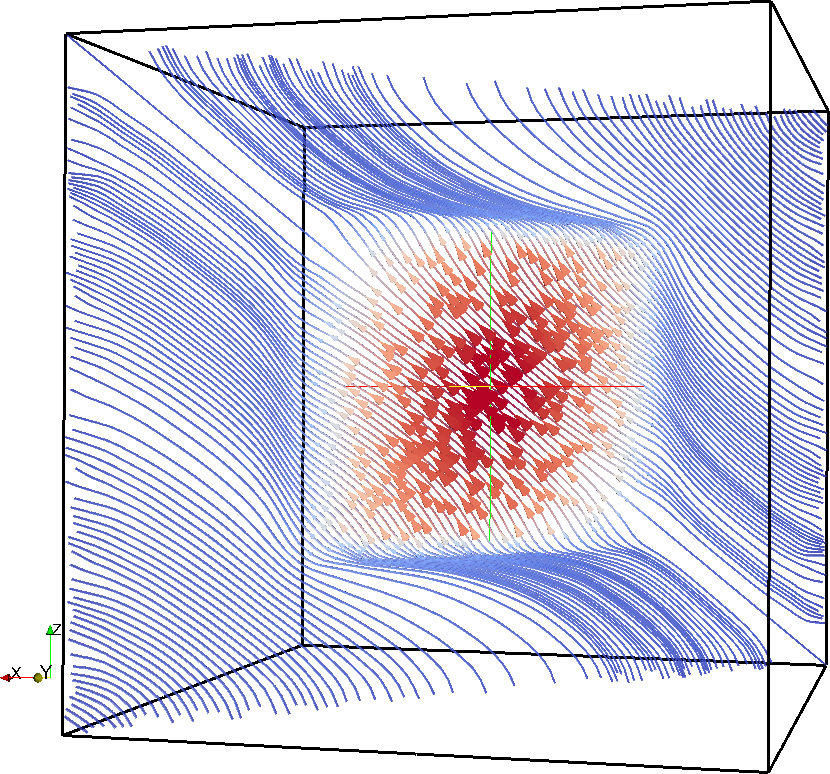
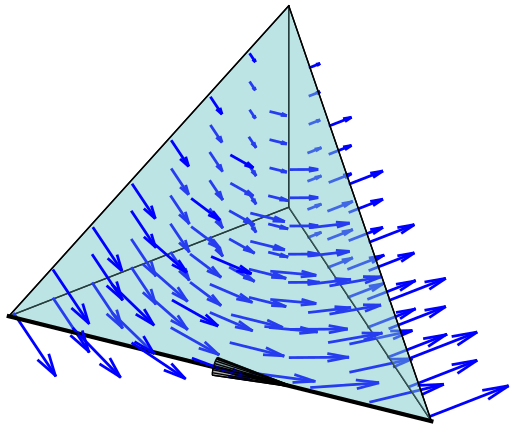
Blog posts

• Notes on the explicit construction of a Helmholtz decomposition
• Boundary conditions for a two-dimensional toy problem
• Deriving the expression of the Lorentz force using the language of a mathematician

References

1. Cao, S., Chen, L. and Huang, X. (2021) “Error analysis of a decoupled finite element method for quad-curl problems,” Journal of Scientific Computing, 90(1). doi: 10.1007/s10915-021-01705-7.

   @article{CaoChenHuang2021quadcurl,
     title = {Error analysis of a decoupled finite element method for quad-curl problems},
     author = {Cao, Shuhao and Chen, Long and Huang, Xuehai},
     journal = {Journal of Scientific Computing},
     volume = {90},
     number = {1},
     year = {2021},
     month = nov,
     doi = {10.1007/s10915-021-01705-7},
     arxiv = {https://arxiv.org/abs/2102.03396},
     code = {https://github.com/lyc102/ifem/tree/master/research/quadCurl}
   }

   Finite element approximation to a decoupled formulation for the quad–curl problem is studied in this paper. The difficulty of constructing elements with certain conformity to the quad–curl problems has been greatly reduced. For convex domains, where the regularity assumption holds for Stokes equation, the approximation to the curl of the true solution has quadratic order of convergence and first order for the energy norm. If the solution shows singularity, a posterior error estimator is developed and a separate marking adaptive finite element procedure is proposed, together with its convergence proved. Both a priori and a posteriori error analysis are supported by the numerical examples.
   
   
2. Cao, S., Wang, C. and Wang, J. (2022) “A New Numerical Method for Div-Curl Systems with Low Regularity Assumptions,” Computers & Mathematics with Applications, 114, pp. 47–59. doi: 10.1016/j.camwa.2022.03.015.

   @article{CaoWangWang2021divcurl,
     title = {A New Numerical Method for Div-Curl Systems with Low Regularity Assumptions},
     author = {Cao, Shuhao and Wang, Chunmei and Wang, Junping},
     journal = {Computers & Mathematics with Applications},
     volume = {114},
     pages = {47-59},
     year = {2022},
     issn = {0898-1221},
     doi = {10.1016/j.camwa.2022.03.015},
     eprint = {2101.03466},
     archiveprefix = {arXiv},
     primaryclass = {math.NA},
     arxiv = {https://arxiv.org/abs/2101.03466},
     code = {https://github.com/lyc102/ifem/tree/master/research/PDWG}
   }

3. Cai, Z., Cao, S. and Falgout, R. (2016) “Robust a posteriori error estimation for finite element approximation to H (curl) problem,” Computer Methods in Applied Mechanics and Engineering. Elsevier, 309, pp. 182–201.

   @article{CaiCaoFalgout2016robust,
     title = {Robust a posteriori error estimation for finite element approximation to H (curl) problem},
     author = {Cai, Zhiqiang and Cao, Shuhao and Falgout, Rob},
     journal = {Computer Methods in Applied Mechanics and Engineering},
     volume = {309},
     pages = {182--201},
     year = {2016},
     publisher = {Elsevier},
     arxiv = {https://arxiv.org/abs/1510.00027}
   }

4. Cai, Z. and Cao, S. (2015) “A recovery-based a posteriori error estimator for H(curl) interface problems,” Computer Methods in Applied Mechanics and Engineering. Elsevier, 296, pp. 169–195.

   @article{CaiCao2015recovery,
     title = {A recovery-based a posteriori error estimator for H(curl) interface problems},
     author = {Cai, Zhiqiang and Cao, Shuhao},
     journal = {Computer Methods in Applied Mechanics and Engineering},
     volume = {296},
     pages = {169--195},
     year = {2015},
     publisher = {Elsevier},
     arxiv = {https://arxiv.org/abs/1504.00898}
   }

   

Finite element methods and other miscellaneous topics

Blog posts

• iFEM project: construction and a MATLAB implementation of the hierarchical basis for linear finite elements
• Kernels of a bounded operator’s extension
• The well-posedness of Robin boundary value problems
• An example on the limiting case of Sobolev embedding
• The little warming up project: the discontinuous Galerkin method for linear advection equation