Discontinuous Galerkin method for linear advection equation

PDE

This was the first project after I switched to a PhD program in computational math. The goal of the project is to study the Discontinuous Galerkin (DG) finite element method for the pure advection problem below, and to investigate various choice of the a posteriori error estimation for it.

\[\left \{ \begin{aligned} \nabla \cdot(\boldsymbol{\beta} u) + \mu u &= f &\text{in } \Omega,\quad \\ u &= g & \text{ on } \partial \Omega^{-}. \end{aligned}\right.\]

Discretization

The discontinuous Galerkin discretization is:

\[a_h(u,v) = \sum_{K\in \mathcal{T}_h} \int_K (\mu u + \boldsymbol{\beta}\cdot \nabla u)v + \int_{\mathcal{F}^i_h} |\boldsymbol{\beta} \cdot \boldsymbol{n}|(u^+ - u^-)v^+ + \int_{\partial \Omega^-} |\boldsymbol{\beta}\cdot \boldsymbol{n}| uv, \tag{1}\]

Now let $W_h$ be the discontinuous finite element approximation space, the finite dimensional approximation is:

\[\left\{ \begin{aligned} &\text{Find } u_h \in W_h \text{ such that } \\ &a_h(u_h, v_h) = \int_{\Omega} fv_h + \int_{\partial\Omega^-} |\boldsymbol{\beta}\cdot \boldsymbol{n}| \,g\,v_h \quad \text{ for any } v_h \in W_h. \end{aligned} \right.\]

By a simple post-processing of averaging $\boldsymbol{\beta} u_h$ near a vertex, the error can be accurately estimated a posteriori:

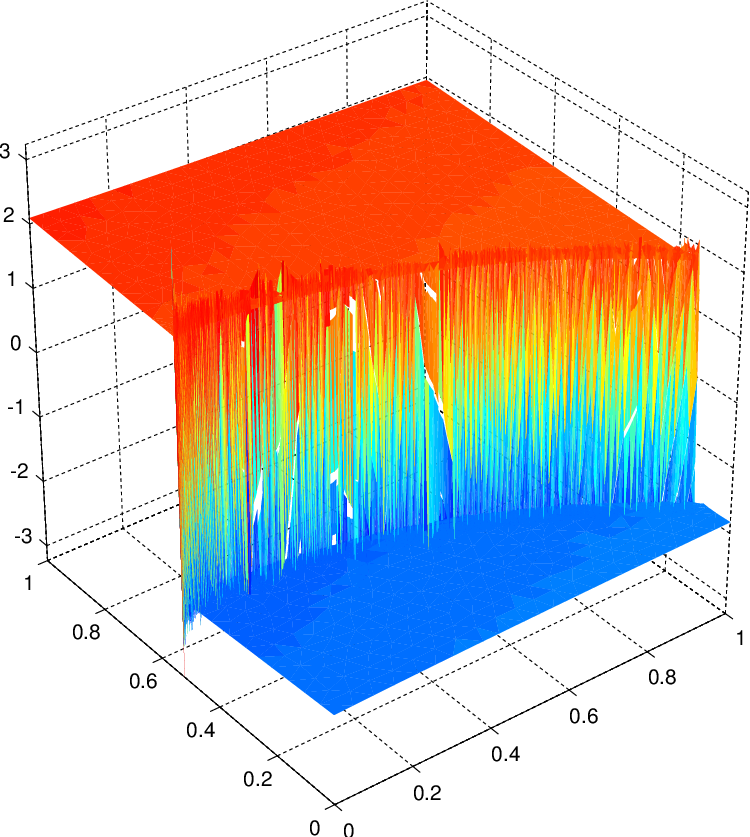
\[\eta_K = h^{-1/2}_K \|G(\boldsymbol{\beta} u_h) - \boldsymbol{\beta} u_h\|_{0,K} \approx \text{error near element } K\]

The result looks promising, as the estimator above can accurately guide the finite element method to refine the mesh near the shock layer, yet the lowest order DG method suffers from some oscillatory artifacts near the discontinuity.

A good coding practice

Coding this method helped me hone the coding skill from the for loop mindset to being familiar with vectorization (for scripting language like Matlab/Python/Julia), and found this gem that has been impacting my research ever since:

L. Chen. iFEM: An innovative finite element method package in Matlab. Technical report, University of California-Irvine, 2009.

For example, the following code snippet checks the inflow condition (the $\mathcal{F}^i_h$) in $(1)$ in a vectorized fashion without a for loop iterating around every triangle in the figure above:

B = sparse(Ndof,Ndof);
% B is the stiffness matrix for B(u,v) on interior edges
% B(u,v) = \sum_{e\in F^i} \int_e |\beta \cdot n| (u^{+} - u^{-}) v^{+}

temp2x = quadedge(node, intEdges, beta_x);
temp2y = quadedge(node, intEdges, beta_y);

% inflow indicator for node i and j near an edge
% the index follows e2v respectively for i and j
% i-th column nodal basis on the inflow = 1, outflow = -1
% j-th column nodal basis on the inflow = 1, outflow = 0

temp_e_x = normalvec_e2v(:,1).*beta_x(e2v_midpt);
temp_e_y = normalvec_e2v(:,2).*beta_y(e2v_midpt);
temp_e = temp_e_x + temp_e_y;

inflow_indicator_i(:,1) = (temp_e <= 0) - (temp_e > 0);
inflow_indicator_i(:,2) = inflow_indicator_i(:,1);
inflow_indicator_i(:,3:4) = -inflow_indicator_i(:,1:2);
inflow_indicator_j = 0.5*(inflow_indicator_i + 1);

for i = 1:4
    for j = 1:4

        %check whether i-th column and j-th column are the same nodes
        edgenode_match = node_dg(e2v_int(:,i),:) == node_dg(e2v_int(:,j),:);
        edgenode_check = edgenode_match(:,1).*edgenode_match(:,2);

        if edgenode_check == 1

            % if the e2v(:,i) is node1 in edge, use temp(:,1)
            % if the e2v(:,i) is node2 in edge, use temp(:,2)
            % is1node and is2node are the indicators of whether the entries in
            % e2v(:,i) is the starting node or not
            match1 = (node_dg(e2v_int(:,i),:)==node(intEdges(:,1),:));
            match2 = (node_dg(e2v_int(:,i),:)==node(intEdges(:,2),:));
            is1node = match1(:,1).*match1(:,2);
            is2node = match2(:,1).*match2(:,2);

            B1ij = is1node.*(temp2x(:,1).*normalvec_e2v(:,1) + temp2y(:,1).*normalvec_e2v(:,2));
            B2ij = is2node.*(temp2x(:,2).*normalvec_e2v(:,1) + temp2y(:,2).*normalvec_e2v(:,2));

            Bij = (abs(B1ij) + abs(B2ij)).*inflow_indicator_i(:,i).*inflow_indicator_j(:,j);
        else
            % if i-th and j-th column of e2v are different node use temp(:,3)
            B3ij = temp2x(:,3).*normalvec_e2v(:,1) + temp2y(:,3).*normalvec_e2v(:,2);
            Bij = abs(B3ij).*inflow_indicator_i(:,i).*inflow_indicator_j(:,j);
        end
        B = B + sparse(e2v_int(:,i),e2v_int(:,j), Bij, Ndof, Ndof);
    end
end