关于《星际穿越》里面的一些物理相关的计算:1小时等于7年的时间差可能吗?etc
这是很久以前在果壳小组写的外行解读帖子,现在果壳小组没有了,把自己以前给果壳写的帖子留个备份。
Caveat lector:本文有影响阅读的数学术语,和《星际穿越》的情节。
自己终于看到的索恩写的那本书《The Science of Interstellar》,因为考虑到读者,大部分公式和计算都被略去了。这篇文章算是一些补充。 首先,《星》是考虑过已知的物理,计算考证过片中出现的一些情节的可能性的,这已经和大部分科幻电影划分了界限;然后对于未知的物理则给出了戏剧化但是又基于已知物理的表现。然后,本文对吹毛求疵挑bug批评剧情台词设计也不感兴趣。下面进入正题。
关于黑洞的一些小知识
黑洞是一颗恒星,已经燃尽生命,塌缩成了弯曲的时空。 黑洞的中心叫奇点(Singularity),奇点外面被视界(Event horizon)包裹住,在视界上的逃逸速度是光速。一粒在视界上的光子可以绕着视界转动永远不会离开,如果你在远处观察一个落入视界的物体你会发现它静止在视界上,仿佛时间停止了一般。视界以内是什么样的,目前理论上没有定论,更别说实际观测。 黑洞并不会把周围的东西都吸进去,真实宇宙中的黑洞也像太阳系中的太阳一般都是在自己旋转着,并且有星体围绕其做圆周运动。和9大行星围绕太阳旋转不同,黑洞周围的椭圆轨道上的有些是恒星系。不同质量的黑洞扮演着不同的角色,比如天鹅座X-1黑洞(Cygnus X-1)是一颗超巨星的伴星;又比如60年代用射电天文望远镜发现的我们所在的银河系中心有着4亿个太阳质量的巨大黑洞。《星》中的黑洞卡冈图(Gargantua)是前者,和其旁边的中子星庞古艾(Pantagruel)组成一个双星系统。 黑洞有着巨大的引力“密度”,但这些引力不是由具体某种物质的质量造成的,而是巨大的引力势能(能量即质量),把周围的时间和空间都扭曲了,并且这些势能被储存在扭曲的时空中。这里我们可以把空间想象成一张弹性薄膜,引力势能就好比弹性势能,参考视频:
旋转不带电荷的黑洞会把物质从赤道面以环形轨道卷入,然后从自转轴两极的喷出。赤道面的圆环,叫做吸积盘。就是如下的效果(图片来源NASA,Biretta et al., Hubble Heritage Team (STScI /AURA)):

引力不同的地方时间的流逝的快慢
在去找Miller小队去到的巨浪星之前,片中提到的一个令人震撼的时间差:巨浪星上1小时等于地球上7年。可能有同学会问,什么样的情况,才会有1小时等于7年时间差?狭义相对论中,有一个洛伦兹因子$\gamma$:
\[{\displaystyle \gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\frac {1}{\sqrt {1-\beta ^{2}}}}={\frac {dt}{d\tau }}}\]这个公式告诉我们,选取一个惯性参照系(可以看成一个“静止”的物体)的话,一个物体A正在以速度$v$远离着相对于这个参照系静止的一个物体B,那么在这个运动物体A上,钟会走得更慢;如果B物体经过了1秒,那么A物体上,钟则会走过$\gamma$秒。
电影中,1小时等于7年的时间差大约是61360,代入上式$\gamma$,解得
\[v \approx 0.9999999998672 c\]要知道这里$c$是光速。 难道巨浪星的公转速度要接近光速?!这怎么可能呢?索恩在他的《The Science of Interstellar》里面给出了答案: 在广义相对论中,引力是是被弯曲的时空所描述,而时间的流逝之相对倍率是由不同观测者身处位置的引力所决定。如果巨浪星在一个自旋速度极快的黑洞旁边,这样的时间流逝速度倍率是有可能的。
这里关于上面的论断我做出一点补充:真实宇宙中,不存在惯性参照系,狭义相对论的时间流逝的洛伦兹因子公式只是引力“密度”较小时候对真实时间流逝差的近似。索恩在书中没有提到计算的细节,这里我们可以利用影片中的一些线索补全。第一个细节是黑板的图片:
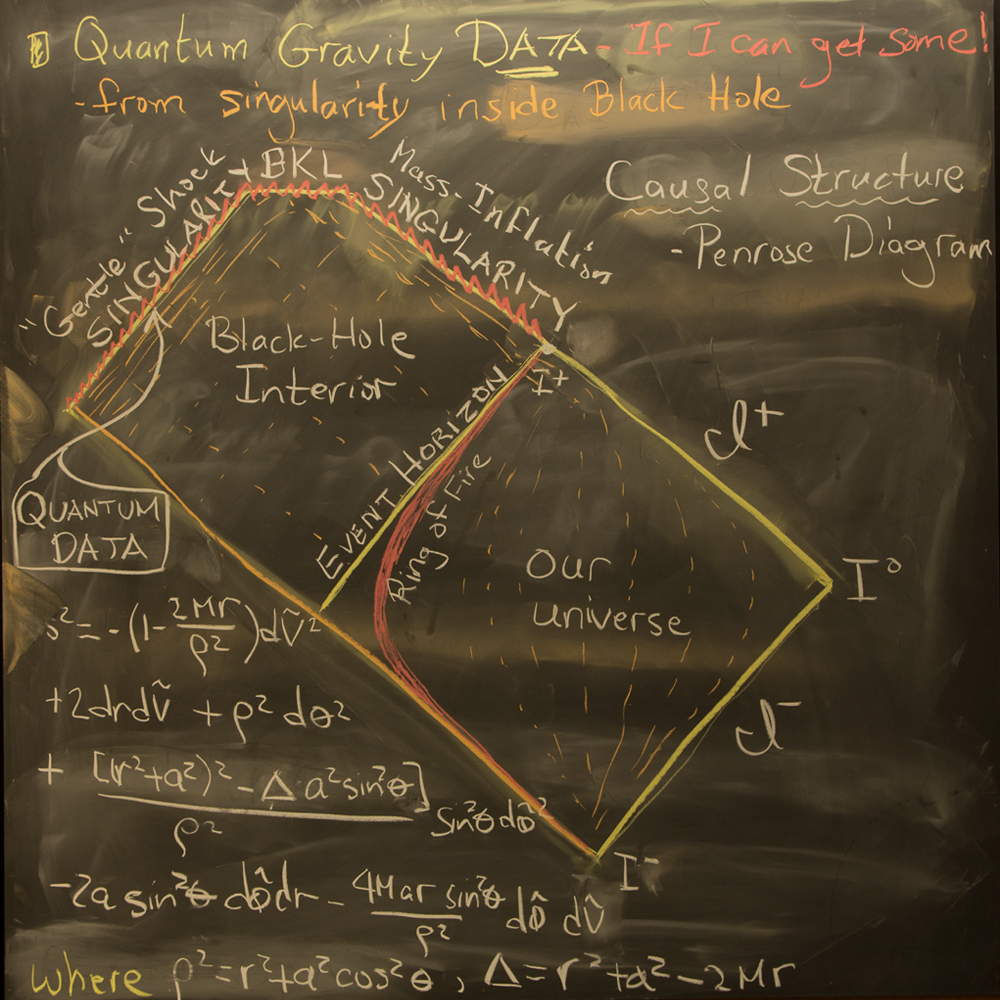
注意黑板右下角的公式就是传说中的科尔-纽曼度规(Kerr-Newman metric。这个度规是描述一个有自旋的黑洞周围的时空是如何弯曲的,是爱因斯坦场方程在假设了黑洞“形状”的性质之后的特殊解(比如假设黑洞处于均衡稳定态,并且是关于自转轴对称的;并且还要分离4维时空坐标为1维时间+3维空间)。
\[ds^{2}_{\mathrm{KN}}=\left(1-\frac{2Mr-Q^2}{R^2}\right)du^{2}+2du\,dr+2\frac{a\sin^{2}\theta}{R^2}\left(2Mr-Q^2\right) du\,d\phi \\ -2a\sin^{2}\theta \,dr\,d\phi-R^{2}d\theta^{2}+\frac{\sin^{2}\theta}{R^2}\left(\Delta a^{2}\sin^{2}\theta-(a^2+r^2)^2\right)\,d\phi^{2}.\]其中$M$是黑洞的质量,$Q$是黑洞所带的电荷总量,$a = J/M$是单位质量的角动量。其中$ds^{2}$是所谓的线微分量(line integral element),也是说在弯曲时空中走一小段“路程”,这一小段“路程”是被哪些量所影响的。等式右边的微分量来源于Boyer-Lindquist坐标系,即一个几乎不受引力影响的时间坐标$t$,加上一个和自转轴垂直的径向被自旋压扁了的球坐标系。还有两个参量分别是
\[\rho^{2}\equiv r^{2}+a^2\cos^{2}\theta, \qquad \Delta\equiv r^{2}+a^2-2Mr+Q^2.\]黑板上的式子假设了电荷是$Q=0$(?比较奇怪的假设可能方便计算),在半径$r$较大,并且电荷数$Q$是0的时候,科尔-纽曼度规近似简化成了科尔度规(Kerr metric):
\[d s^{2}=\left(1-\frac{r_{s} r}{\rho^{2}}\right) c^{2} d t^{2}-\frac{\rho^{2}}{\Delta} d \tau^{2}-\rho^{2} d \theta^{2}-\left(r^{2}+\alpha^{2}+\frac{r_{s} r \alpha^{2}}{\rho^{2}} \sin ^{2} \theta\right) \sin ^{2} \theta d \phi^{2}+\frac{2 r_{s} r \alpha \sin ^{2} \theta}{\rho^{2}} c d t d \phi \tag{1}\]其中新增的$r_s$是静止的黑洞的施瓦西半径(Schwarzschild radius),也即是假设光速是逃逸速度的半径:
\[v_{\mathrm{escape}}=c=\sqrt{\frac{2 G M}{r_{s}}} \tag{2}.\]小插曲1:上面逃逸速度的获得,实际上是解一个经典的牛顿第二定律所导出的微分方程:
\[F=\frac{G M m}{\left(r_{s}+x\right)^{2}}=m a=m \frac{d v}{d t}=m \frac{d x}{d t} \frac{d v}{d x}=m v \frac{d v}{d x}\]
其中$x$是距离黑洞视界的径向距离(距离视界的“高度”)。解这个微分方程可以得到一个$v$关于$x$的函数。最后得到那个解我们要假设$v$在$x$趋于无穷远处的时候趋于0。这样假设的原因是$v$不在有限距离内为$0$,说明逃脱了引力$F$;如果在有限距离为0的话,再微弱的引力也会把这个物体拉回去。
现在我们终于可以开始计算由于弯曲时空表现出来的引力造成的时间流逝差了:在科尔度规$(1)$中: 令$dtd\phi=0$,也即是说我们现在考虑一个对于角度静态的观测者(空间相对极角位置没有变化),我们可以立即得到在黑洞旁的扭曲时空中走一段“路程”所用的“时间”
其中$d\tau$是黑洞旁时间的流逝),与$dt$(远离该黑洞引力影响的时间)的时间差:
\[\left(\frac{d \tau}{d t}\right)^{2}=1-\frac{r_{s} r}{\rho^{2}}\]把(2)和rho和a的定义代入该式我们可以得到
\[\frac{2 G M r}{r^{2}+J^{2} \cos ^{2} \theta / M^{2}}=1-\left(\frac{d \tau}{d t}\right)^{2} \tag{3}\]上面这个方程可以看成一个代数方程而非微分方程,我们开始往这个方程里面代入参数。 影片中提到巨浪星上1小时就是地球上7年: 索恩在《The Science of Interstellar》中提到《星》中的黑洞卡冈图的质量大约是1亿个太阳质量:$M \approx 2\times 10^{38}$ kg, 并且黑洞的自旋接近极限速度。为简化计算,假设观测者在黑洞的自转轴的方向上 $\cos\theta=1$。我们可以得到轨道半径的近似解:
\[r = 3.5\times 10^{11} \mathrm{m}.\]索恩在书中提到卡冈图视界“半径”大约是1.5e9米;嗯……离视界好像还有段距离。慢着,索恩是在书中提到这个数字,是在四维空间中的bulk中测量的;这里我照了张索恩在《黑洞与时间弯曲》的书里面的一张图:
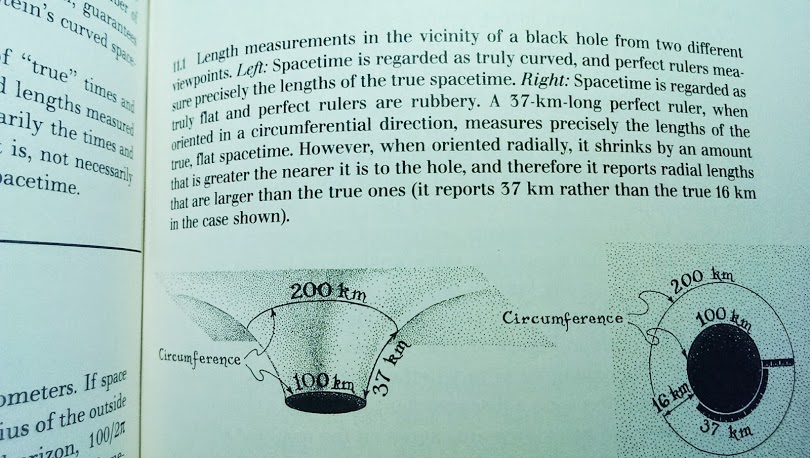
上面的图是类比3维扭曲空间镶嵌到4维空间画成的2维扭曲空间镶嵌到3维空间,半径是由上图中的周长(circumference)除以$2\pi$得到。所以不是真正的径向距离。另外一张帮助理解的图可以参考索恩网站上的插图:
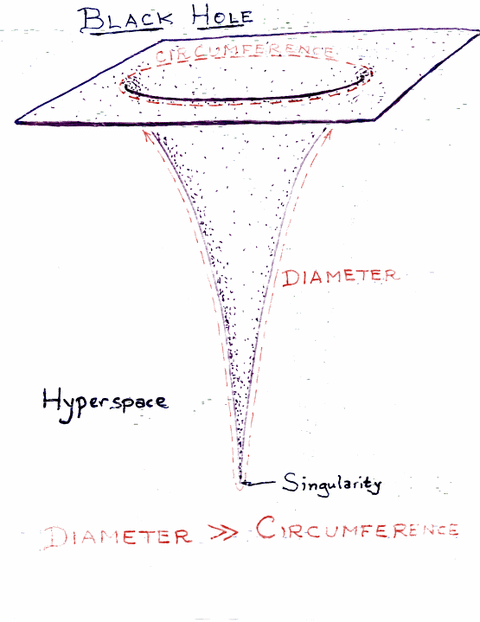
上图中的Hyperspace便是《The Science of Interstellar》中的bulk:镶嵌到四维空间之后,可以看到因为扭曲的时空,黑洞周围的轨道周长不能再用$r$来计算了。索恩在书中给出的1.5e9的半径,可以看作是上图中顶部那个圆环的长度除以$2\pi$。而我们计算出来的半径则是上图中那个diameter的一半。实际的周长,依然可以用度规计算:在$(1)$ 的Kerr度规中,令$dr=0$,并且假设$\theta=\pi/2, d\theta = 0$,对$\phi$从0到$2\pi$积分。也即是说我们想象自己站在黑洞的赤道上绕黑洞走一个大圆。
参考Taylor-Wheeler的天体物理教课书《Exploring Black Holes》,可以得到假设两个重要常数都没单位的情况下,也即是$G=c=1$的时候,令(1)式上面的$\Delta=0$,这个代数方程大的那个根就是带有自旋黑洞的半径:
\[r_{+}=\frac{G M}{c^{2}}+\frac{1}{c} \sqrt{\left(\frac{G M}{c}\right)^{2}-a^{2}}\]当黑洞没有自旋的时候,$a=0$,我门便又回到光速为逃逸速度的施瓦西半径$(2)$。但是如果第二项黑洞自旋速度几乎是极限速度,根号下那个基本可以忽略不计的话:
\[r_{+} \approx \frac{G M}{c^{2}}=\frac{1}{2} r_{s}\]极限自旋的黑洞半径应该几乎是施瓦西半径的一半。经过计算我们发现这个数是$10^{11}$米量级的。
注2:对于远处的观测者来说,周长公式则不被影响太多,周长变长和时间流动变快的这个效应有个相互抵消作用;根据《The Science of Interstellar》书中文字,在远处观测到的巨浪星公转周期是1.7个小时,公转速度是0.55倍光速,我们可以算得半径也是$10^{11}$米量级的。 再次根据Taylor-Wheeler的《Exploring Black Holes》里面给出的黑洞周围轨道周期公式得到在巨浪星上测出公转周期大约是0.1秒……(基本符合索恩书中给出的数字,见《The Science of Interstella》第17章165页)。 很多同学会问,一个自转周期如此之短的行星怎么能够登陆?答案是使用两次重力弹弓,第二次是用到卡冈图黑洞的中子星伴星庞古艾减速(参考《The Science of Interstellar》第7章)。 最后,关于巨浪星所在轨道的位置,实际上是应该在吸积盘以内的,应该在上图中ISCO( innermost stable circular orbit,靠近黑洞的极限稳定轨道)所在位置。大家可以参考Physics.SE上关于这点的讨论。
落入黑洞之后怎么办?
自己在网上看到很多质疑的声音,其实我也不知道。 但是这里告诉大家一个关于黑洞数学上有趣的结果: 在Kerr度规中,如果令$\rho^2=0$,这也是黑洞物理奇点的位置。我们发现,这个奇点实际上是赤道面的一个圆环!:$r=0$, $\theta=\pi/2$。 在这种环形奇点旁边,哥德尔在1949年在满足Kerr度规的黑洞进一步特殊化之后,得到了场方程在3+1时空用柱状坐标的特殊解:
\[d s^{2}=-\mathrm{d} t^{2}+\mathrm{d} \tau^{2}+\mathrm{d} z^{2}-\sinh ^{2} r\left(\sinh ^{2} r-1\right) \mathrm{d} \phi^{2}+\sqrt{2} \sinh ^{2} r(\mathrm{d} \phi \mathrm{d} t+\mathrm{d} t \mathrm{d} \phi)\]这个解被认为是“unphysical”的闭合时间曲线的解;也即是,穿越到过去。从时空中的一点出发,跨越了时间和空间又回到了时空中的这个点。 当然这只是数学上的可能,关于时间旅行的有趣思想实验,可以参考索恩的《黑洞与时间弯曲》第14章(。 《星》最后时间维度变为空间维度之后的超立方体视觉效果真是令人赞叹……如果对于这点有所怀疑的同学可以去参考索恩《The Science of Interstellar》的第22章和第29章。 《The Science of Interstellar》书中提到的《Flatland》,著名科普作家Carl Sagan曾经制作了一个短片帮助身为3维生物的咱们理解4维空间,这里也力荐给大家:
文章的尾声,有一个连接,有兴趣的读者可以点进去看看:https://interstellar.withgoogle.com/for-educators (这个链接现在已经没有了)
这是Interstellar制片方和Google联合制作的一个关于《星》中蕴含的科学知识的学习网站,提供给老师们教中学生甚至是小学生的课件:从维度,计算距离,摩斯电码,到荷马史诗。 索恩在《The Science of Interstellar》中提到他最初构思影片的初衷是激发年轻一代的物理的兴趣而从事科学事业;对自己来说,索恩在《黑洞与时间弯曲》已经做到了;《星》这部电影还有待时间的检验。 自己很期待将来有一位推动人类太空事业发展的科学家说:“我小时候看了《星际穿越》,那是让我成为科学家为人类做出贡献的源动力之一。”
小附注:在《黑洞与时间弯曲》开篇的科幻“小说”中,那个潮汐力基本可以忽略不计的巨大黑洞就叫卡冈图。

参考资料:
- The Kerr spacetime: A brief introduction, M. Visser, http://arxiv.org/pdf/0706.0622.pdf.
- Wikipedia关于Kerr Metric和Kerr-Newman metric的条目.
- Ikjyot Singh Kohli的博客: ikjyotsinghkohli24.wordpress.com.
- The Science of Interstellar, K. Thorne.
- Exploring Black Holes: Introduction to General Relativity, E. Taylor, J. Wheeler.



Comments